Я решил разделить описание алгоритмов с их реализациями. Поэтому здесь описаны только алгоритмы без примеров и замечаний к реализации.
Определение диаграммы Вороного процитирую с Википедии:
Определение диаграммы Вороного процитирую с Википедии:
Диаграмма Вороного конечного множества точек S на плоскости представляет такое разбиение плоскости, при котором каждая область этого разбиения образует множество точек, более близких к одному из элементов множества S, чем к любому другому элементу множества.Опишу несколько свойств диаграммы Вороного, которыми я скорее всего буду пользоваться дальше:
- Диаграмма Вороного - это планарный граф. С помощью теоремы Эйлера можно несложно доказать, что если диаграмма Вороного построена на множестве из n точек, то она содержит O(n) ребер и вершин (я знаю доказательство, которое использует тот факт, что степень каждой вершины хотя бы 3).
- Ячейка диаграммы Вороного для точки P является пересечением полуплоскостей, образованных серединными перпендикулярами отрезков вида [A;P] (A - точка из нашего множества) и содержащих точку P.
 |
| Синим выделена ячейка Вороного для точки G edge - это ребро диаграммы Вороного vertex - вершина |
Все приведенные ниже алгоритмы будут строить лишь множество ячеек Вороного, не объединяя их в общий планарный граф.
Соответственно, самый просто алгоритм за O(n4)
В данном алгоритме используется тот факт, что количество ребер в диаграмме Вороного - O(n).
Действительно, если бы мы научились находить каждое ребро одной ячейки Вороного за время T(n), то мы автоматически придумываем алгоритм построения диаграммы Вороного за O(n T(n)). Круто =)
Давайте начнем придумывать. Для начала хочется от чего-то оттолкнуться. Действительно, найдем такую точку, которая по любому есть в ячейке Вороного для данной точки. Эта точка несложно ищется - давайте среди всех середин отрезков M = (середина [P;A], где P - выбранная точка, A - любая другая точка из исходного множества) выберем ближайшую. Утверждается, что эта точка точно присутствуем в ячейке для точки P (т.е. она лежит на границе многоугольника, который мы хотим найти). Если таких точек несколько - возьмем любую.
Замечательно, теперь у нас есть опорная точка и опорная прямая, т.к. серединный перпендикуляр отрезка, на котором мы взяли ближайшую точку, является ребром результирующего многоугольника.
Теперь поймем, как по прямой, содержащей ребро ответа и точке на ребре узнать следующее ребро. Ну это не сильно сложно. Давайте пересечем все остальные серединные перпендикуляры с текущей прямой. Возьмем 2 (или 1) точки пересечения - самый ближайшие точки с каждой из сторон к текущей точке на ребре (см. рисунок срочно!):
Разберем немного рисунок. Точка K - опорная точка. Мы пересекли четыре серединных перпендикуляра. P, Q - точки пересечения с прямой f, причем самые ближайшие к точке K. Понятно - что эти точки являются вершинами конечного многоугольника, а серединные перпендикуляры, их содержащие - следующими ребрами. Поэтому достаточно запустить рекурсивную функцию от изменившихся параметров - точки P и прямой n и точки Q и прямой j.
Более формально, угол между направлением нового ребра и направлением на точку, около которой строим ячейку, должен быть минимален (на рисунке выделен зеленым).
Таким образом, мы каждое ребро мы научились строить за O(n). Т.е. итоговая асимптотика такая, какую я заявил в начале рассказа про этот алгоритм =)
На этом данный пост кончается. Мне кажется в нем даже чересчур много инфы.
Хочу напомнить, что в данном посте я не стремился указать на способы реализации описанных алгоритмов. Моей задачей было ознакомить читателя с идеями =)
Соответственно, самый просто алгоритм за O(n4)
- Зафиксируем точку, ячейку Вороного которой мы хотим построить - точка P.
- Построим все серединные перпендикуляры отрезков вида [A;P].
- Пересечем все серединные перпендикуляры между собой.
- Для каждой точки пересечения проверим, что она принадлежит каждой полуплоскости. Точку, лежащую во всех полуплоскостях, назовем подходящей.
- Отсортируем все подходящие точки по полярному углу.
- Полученное множество точек - ячейка Вороного точки P.
Видно, что для каждой точки ячейка построится за время O(n3) (для каждой из точек пересечения, которых порядка n2, мы делаем проверку за n; алгоритм сортировки в таком случае не портит асимптотику).
Из картинки видно, что ячейка Вороного может быть бесконечной. Данный случай можно определить однозначно по существованию "разрыва" - пары последовательных точек в нашем отсортированном списке, угол между которыми не меньше 180°. |
| угол обозначенный зеленым цветом - "разрыв" |
Далее разберем на словах алгоритм за O(n3).
В основе этого алгоритма лежит идея пересечения n полуплоскостей за квадрат. Как это делать?
Известно, что пересечение полуплоскостей - это выпуклый многоугольник (возможно бесконечный, как на рисунке). Тогда алгоритм пересечения за квадрат следующий:
В основе этого алгоритма лежит идея пересечения n полуплоскостей за квадрат. Как это делать?
Известно, что пересечение полуплоскостей - это выпуклый многоугольник (возможно бесконечный, как на рисунке). Тогда алгоритм пересечения за квадрат следующий:
- На i-ой итерации алгоритма будем строить многоугольник, являющийся пересечением первых i полуплоскостей.
- Чтобы перейти от i-ой итерации к следующий нужно пересечь текущий многоугольник с полуплоскостью. Это можно сделать за время, пропорциональное текущему количеству вершин в многоугольнике. Для этого заметим, что новый многоугольник - это некоторая непрерывная последовательность вершин старого многоугольника и, иногда, ещё две новые вершины по краям (для лучшего понимания можно попробовать исследовать рисунок).
 |
| Пересекаем многоугольник с зеленой полуплоскостью |
 |
| Вуа-ля! Пересекли. Добавились точки J, K. От старого многоугольника остались точки E, D, C. |
Дальше - больше! Перед Вашими глазами сейчас предстанет алгоритм алгоритм за O(n2logn).
Идея та же, что и в предыдущем алгоритме - пересечение полуплоскостей. Только можно сделать это оптимальнее - за nlogn.
Вспомним, что у нас есть. Мы для каждой точки хотим пересечь n полуплоскостей за nlogn. Заметим, что многоугольник пересечения полуплоскостей можно задавать массивом полуплоскостей, обладающим таким свойством - точка пересечения прямых, образующих пары соседних полуплоскостей - это вершина искомого многоугольника (см. рисунок для лучшего понимания).
Идея алгоритма состоит в следующем:
Идея та же, что и в предыдущем алгоритме - пересечение полуплоскостей. Только можно сделать это оптимальнее - за nlogn.
Вспомним, что у нас есть. Мы для каждой точки хотим пересечь n полуплоскостей за nlogn. Заметим, что многоугольник пересечения полуплоскостей можно задавать массивом полуплоскостей, обладающим таким свойством - точка пересечения прямых, образующих пары соседних полуплоскостей - это вершина искомого многоугольника (см. рисунок для лучшего понимания).
 | |||||||
| Выделенный многоугольник можно задать последовательностью | I, III, IV, V |
- Отсортируем полуплоскости по углу нормального вектора. (в случае равенства угла порядок полуплоскостей не будет иметь значения).
- Будем поддерживать массив полуплоскостей, задающий многоугольник-пересечения первых i полуплоскостей (уже отсортированных).
- Чтобы добавить новую полуплоскость нам, возможно, понадобится удалить несколько последних вершин текущего многоугольника, т.к. они не принадлежат новой полуплоскости.
- В конце нужно добавить новую полуплоскость в конец массива.
Ниже приведена gif-анимация процесса построения пересечения полуплоскостей (они пронумерованы римскими числами в порядке сортировки).
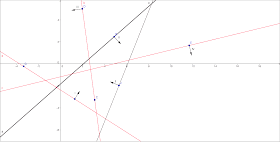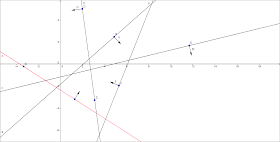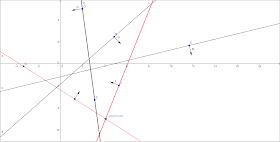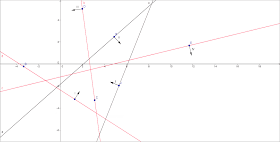 |
| В процессе добавления полуплоскости III мы должны удалить полуплоскость II, т.к. она добавляет плохую точку BADPOINT |
Асимптотика данного алгоритма складывается из двух частей:
- Отсортировать все полуплоскости - O(nlogn)
- Пробег по отсортированному массиву с добавлением и извлечением из стэка. Заметим, что каждая полуплоскость будет добавлена в стэк ровно 1 раз, соответственно удалена тоже не больше одного раза. Итого данная часть алгоритм работает за O(n).
В данном алгоритме используется тот факт, что количество ребер в диаграмме Вороного - O(n).
Действительно, если бы мы научились находить каждое ребро одной ячейки Вороного за время T(n), то мы автоматически придумываем алгоритм построения диаграммы Вороного за O(n T(n)). Круто =)
Давайте начнем придумывать. Для начала хочется от чего-то оттолкнуться. Действительно, найдем такую точку, которая по любому есть в ячейке Вороного для данной точки. Эта точка несложно ищется - давайте среди всех середин отрезков M = (середина [P;A], где P - выбранная точка, A - любая другая точка из исходного множества) выберем ближайшую. Утверждается, что эта точка точно присутствуем в ячейке для точки P (т.е. она лежит на границе многоугольника, который мы хотим найти). Если таких точек несколько - возьмем любую.
 |
| K - ближайшая точка для G |
Теперь поймем, как по прямой, содержащей ребро ответа и точке на ребре узнать следующее ребро. Ну это не сильно сложно. Давайте пересечем все остальные серединные перпендикуляры с текущей прямой. Возьмем 2 (или 1) точки пересечения - самый ближайшие точки с каждой из сторон к текущей точке на ребре (см. рисунок срочно!):
Разберем немного рисунок. Точка K - опорная точка. Мы пересекли четыре серединных перпендикуляра. P, Q - точки пересечения с прямой f, причем самые ближайшие к точке K. Понятно - что эти точки являются вершинами конечного многоугольника, а серединные перпендикуляры, их содержащие - следующими ребрами. Поэтому достаточно запустить рекурсивную функцию от изменившихся параметров - точки P и прямой n и точки Q и прямой j.
Не нужно забывать про то, что несколько серединных перпендикуляров могут пересекать прямую в одной точке. В таком случае нужно выбрать тот серединный перпендикуляр, который "круче" заворачивает вокруг исходной точки(около которой строим ячейку).
Более формально, угол между направлением нового ребра и направлением на точку, около которой строим ячейку, должен быть минимален (на рисунке выделен зеленым).
Таким образом, мы каждое ребро мы научились строить за O(n). Т.е. итоговая асимптотика такая, какую я заявил в начале рассказа про этот алгоритм =)
На этом данный пост кончается. Мне кажется в нем даже чересчур много инфы.
Хочу напомнить, что в данном посте я не стремился указать на способы реализации описанных алгоритмов. Моей задачей было ознакомить читателя с идеями =)


в последнем алгоритме скорее всего ошибка, там точка R ближайшая а не Q
ОтветитьУдалитьЕсть вопрос, а если Дан выпуклый многоугольник и нужно построить диаграмму Вороного, как быть и что делать?
ОтветитьУдалитьМожете подсказать?