Доказательство первого закона Кеплера

(на данный момент в этой статье есть много недочетов. я постараюсь исправить это в ближайшее время)

  Наверное, в поисках адекватного доказательства этого закона, я перерыл многие сайты рунета. Однако больше того, что нам рассказали в СУНЦ-е я не нашел, а доказательство рассказанное нашим учителем меня не совсем устраивает.
   И вот сегодня я решил поискать информацию об этом законе в англоязычных источниках. Во-первых, на запрос "proof of Kepler's first law" Google сразу выдал кучу полезных сайтов, в то время как на аналогичный русский запрос поисковые системы находят лишь формулировку этого закона или что-то наподобие "Закон Кеплера - доказательство существования эфира"...

Открыв наиболее понятную статью, я решил разобраться с доказательством. Мне кажется, что это у меня удалось и в этом посте я хочу изложить то доказательство, которое я прочитал (вот ссылка на оригинал).

Итак, сначала оговорим некоторые математические факты, которыми мы будем пользоваться, но доказывать не будем, т.к это чистая математика:

Теперь приступим к самому доказательству.

Рассмотрим полную энергию планеты, обращающейся вокруг некоторой звезды, и находящаяся в данный момент на расстоянии r.

1

Т.к. на систему не действует внешних сил, то энергия сохраняется.

Покажем, что при E <= 0, расстояние от звезды до планеты ограничено.

В самом деле:

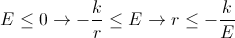2

Таким образом, движение планеты ограничено сферой, с центром в точке O(звезда) и радиусом 

R = -k / E.

Теперь рассмотрим планету, двигающуюся по траектории Q.

Также построим окружность C радиусом R = -k / E.

Заметим, что планета такой же массы, как наша, находящаяся в точке s(и не обладающая кинетической энергией) имеет такую же энергию, как планета, движущаяся по траектории Q и находящаяся в точке r (точки O, s, r лежат на одной прямой). Данное равенство следует из выбора радиуса окружность C.

Обозначим через s - радиус вектор проведенный из точки O в точку s. Тогда s:

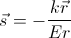3

Построим на рисунке прямую L, совпадающую по направлению с вектором импульса тела(т.е. с вектором скорости) и проходящей через точку r. 

Построим также точку, симметричную точке s относительно прямой L - точку t.

Также на прямой N отметим точку n, такую, что n = L x p

Теорема: вектор t(Ot) постоянен и равен K/mE, где 

4

Доказательство:

Заметим, что вектор t можно получить путем вычитания из вектора s двух векторов j, являющимися проекциями вектора (s - r) на прямую N, которая перпендикулярна прямой L(данный вывод следует из построения точки t, как симметричной точке s относительно прямой L).

Значит:

5

Т.к. (s - r) * n / n  - это проекция вектора (s - r) на прямую N. А n / n - нормированный вектора, направленный вдоль прямой N.

Найдем, чему равно (s - r) * n (подставив значение вектора n и s):

n * n = (L x p) ^ 2 = L^2 * p^2 (это следует из того, что вектор L ортогонален вектору p).

Значит вектор t равен:

Заметим, что вектор t неизменен, т.к. (это я не понял, но к сожалению осознание этого пришло только в момент написания этой строчки. Завтра постараюсь понять и допилить).

Ну и как бы теорема доказана.

Из данной теоремы следует, что

|r - t| + |r - O| = |r - s| + |r - O| = |s|. Т.к. |s| - константа, то мы доказали, что в любой момент сумма расстояний от планеты до двух фиксированных точек - константа. Значит это эллипс. ч.т.д.