Качественные задачи. Часть 5

 Почему крученая шайба преодолевает большее расстояние, чем не крученая?

Будем считать, что на шайбу не дейстувет сила сопротивления воздуха, т.к. она во много раз меньше силы трения скольжения шайбы об лед.

Тогда рассмотрим, как действуют силы на маленький кусочек шайбы:

Сила трения направлена против относительного перемещения. В нашем случае лед не движется, значит сила трения направлена против скорости.

Видно, что сила трения, помимо того, что уменьшает энергию центра масс, также уменьшает энергию данного кусочка относительно центра масс. Такое утверждение истинно для каждого элемента шайбы. Тогда запишем теорему о изменении кинетической энергии, воспользовавшись теоремой Кёнига:

c.o.f - центр масс. fric. - трение. E' - энергий в системе отсчета, относительно центра масс

Т.к. при движении шайбы без вращения изменение кинетической энергии относительно центра масс всегда равно 0 ( т.к. относительно центра масс - шайба неподвижна ), значит при одном и том же перемещении изменение кинетической энергии центра масс в случае вращения будет меньше, чем в случае поступательного движения шайбы. Таким образом, в случае вращения шайбы, сила трения должна совершить большую работу, чтобы остановить шайбу, а значит совершить большее перемещение.

Значит закрученная шайба пролетит большее расстояние, т.к. часть работы силы трения будет уходить на измнение кинетической энергии шайбы относительно центра масс, в то время, как без закручивания, эта работа пошла бы на остановку центра масс.

P.S. Какое-то ужасное и громоздкое решение довольно несложной задачи получилось, господа...

Качественные задачи. Часть 4

   Так уже много частей про качественные задачи, но проку от них маловато)

Почему крученый мяч летит в сторону от той траектории, по которой он бы летел, если бы не имел вращательного движения?

Пусть мяч летит таким образом.

Рассмотрим воздух, находящийся вблизи мяча.
Те молекулы воздуха, которые находятся очень близко от поверхности мяча, увлекается мячом и тоже приобретают некоторую угловую скорость.
Остальные молекулы воздуха остаются неподвижны относительно Земли.

Молекулы воздуха, находящиеся внутри серого круга, имеют угловую скорость w'.

Перейдем в систему отсчета, которая движется также, как центр масс мяча. Тогда те частицы воздуха, которые были неподвижны относительно Земли, теперь приобрели скорость -v, где v - скорость центра масс.

Тогда заметим, что скорость нижнего потока воздуха будет меньше, чем скорость верхнего, т.к. при сложении линейных скоростей встречного потока и потока, который увлекается движением мяча, в первом случае угол между векторами скоростей > 90, а во втором  < 90 ( из этого следует, что если сложить скорости по правилу треугольника, то косинус угла между отрезками, образующими вектора, для нижнего потока - больше 0, а для верхнего - меньше 0. Значит при одинаковых скоростях результирующая скорость будет больше у верхнего потока).

Фиолетовые стрелки - результирующие скоростей потоков воздуха.

 Теперь немного отвлечемся от мячика. Представим себе участок улицы ( например длиной 100м ), по которому идут люди. Причем известно, что каждую секунду на улицу выходят 10 новых людей. Таким образом, если каждый человек будет идти со скоростью 1м/c, то через 100 секунд на улице будет находится 1000(!) человек. Однако, если каждый человек будет бежать со скоростью 10м/c, то через те же 100 секунд на улице будет находится всего 100 человек. Видно, что чем меньше скорость людей в таком случае, тем больше их "концентрация" на улице. А чем больше концентрация, тем больше вероятность того, что люди будут натыкаться друг на друга, ударяться о дома и т.д.

Молекулы, по видимому, ведут себя также, как и люди на улице. В любом случае, из закона Бернулли следует, что чем меньше скорость жидкости ( или газа ), тем больше давление в данной среде. Таким образом, давление со стороны верхнего потока меньше, чем со стороны нижнего. В следствие этого мяч начнет смещаться вверх ( на рисунке ).

p1 > p2

Несколько качественных задач. Часть 3

  Решил придумать самостоятельно несколько качественных задач. Кончено многие задачи всплыли в моей голове, потому что я читал когда-то про них, но в итоге получился вот аткой список:

• Зачем спортсменам, занимающимся прыжками с шестом, нужно шесты разной жесткости?
• Почему крученый мяч летит в сторону от той траектории, по которой он бы летел, если бы не имел вращательного движения?
• Почему крученая шайба преодолевает большее расстояние, чем не крученая?
• Зачем на мяче для гольфа сделано множество маленьких ушлублений?
• Почему воланчик имеет такую странную форму?
• Зачем игроки в керлинг усердно трут лед, по которому скользит камень?
• Зачем смычок скрипки перед игрой натирают канифолью?
• Зачем у лыж есть канавка, расположенная посередине?
  (http://www.sportlive.su/images/goods/swix/fs-t0401_vignet.jpg)

Возможно, некоторые вопросы я позже разберу.

Ещё одна качественная задача. Часть 2

Вот ещё одна задачка. Постараюсь выкладывать их каждый день ( мотивирует усерднее заниматься физикой ).

Задача 3: Почему продукты легче резать не просто надавливая на нож, а надавливая и двигая нож вперёд-назад?

Поймем, что у каждого предмета есть некоторая константа P – максимальное давление, которое может выдержать данный предмет. При превышении этого порога предмет начинает сильно деформироваться/резаться и т. д.
Также, чтобы не возникало различных разногласий, будем считать, что мы действуем на нож с постоянной силой ( т. е. если мы двигаем нож вперед, то только вперед и т. д. ).
Также, я введу всех в курс дела - вот как я представляю нож:

Нож - это черный контур. Серый цвет - дополнительные построения

S - это площадь нижнего основания нашего ножа.

Рассмотрим случай, когда мы давим на нож, не двигая его.

Тогда формула для давления ножа на наш предмет при условии, что он ( нож ) погрузился на глубину h выглядит как-то так:

Где F – сила, с которой мы действуем на нож; [альфа] – угол «острия» ножа ( посмотрите на рисунок ); S – площадь основания ножа; f([альфа], h) – некоторая функция, которая тем меньше, чем глубже погружается нож и чем больше [альфа] ( просто из жизненного опыта посудите: легче резать тупым или острым ножом; легче резать сначала или потом, когда нож уже погрузился в предмет ).

Теперь рассмотрим случай, когда нож двигается вперед. Тогда сила, с которой мы действуем на нож направлена  не перпендикулярно поверхности предмета, а в строну.

Логично, что сила, с которой нож действует на тело направлена в ту же сторону, что и сила, которую прикладываем мы.

Теперь рассмотрим сечение ножа.

В случае, когда мы не двигаем нож, мы режем предмет «сечением» ABC. Однако, если мы режем предмет, продвигая его в какую-либо сторону, то на предмет оказывает воздействие в данной точке уже сечение DBE. Можно заметить, что [бета] < [альфа] ( я вижу этому такое объяснение: BE > BC и BD > BA – т. к. это наклонная и перпендикуляр. Однако DE = AC. Значит, чтобы выполнялась теорема косинусов для треугольников ABC и BDE, нужно, чтобы cos[бета] > cos[альфа], т. е. [бета] < [альфа] ).

Тогда в этом случае давление будет высчитываться по формуле:

Т.к. [бета] < [альфа], то f([бета], h) > f([альфа], h), значит давление на тело во втором случае больше, значит резать легче, если двигать нож вперед-назад.

P.S. Я довольно долго осознавал это решение и то, что написано в данном посте - лично моё понимание. Здесь ( как и в прошлом посте ) может находится множество ошибок/недочетов и т.п. Если у вас есть какие-нибудь замечания - оставьте комментарий или напишите мне на e-mail: golovoiapklavu@gmail.com

Несколько качественных задач по физике. Часть 1

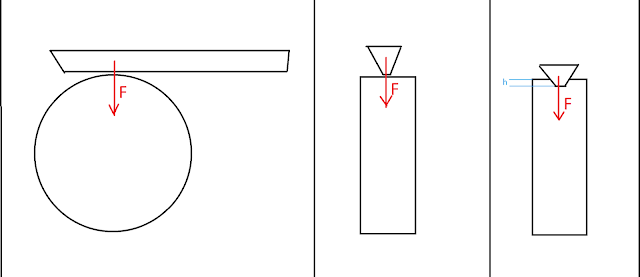
   Около недели осталось до того, как мне сдавать экзамен по физике. Самым сложным в этот раз будет то, что нужно будет решать качественные задачи. Приведу несколько задач с решениями ( решения мои, поэтому в них могут быть недочеты/ошибки и т.п.).

Задача 1: Почему бегущий человек, стремясь быстро и круто обогнуть столб или дерево, обхватывает его рукой?

Для в общих чертах опишем условия, в которых мы будем решать данную задачу:
  Коэффициент трения между подошвой человека и соприкасающейся с ней поверхностью — k ~ 0.5 ( т. к. чаще всего мы имеем дело с таким коэффициентом трения ).
  Также, будем считать, что при огибании столба, человек двигается по окружности постоянного радиуса с постоянной по модулю скоростью.

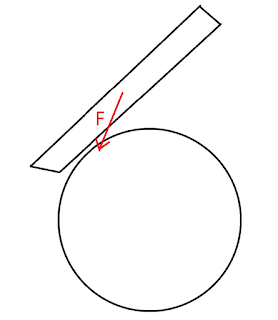
Теперь рассмотрим ситуацию, когда человек огибает столб, не обхватывая его рукой.

Тут, по-моему, все непонятно...

 В этом случае, скорость человек должна быть такой, чтобы выполнялось равенство:

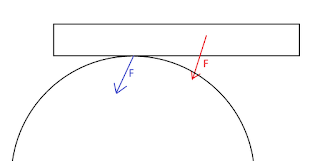
Теперь рассмотрим случай, когда человек обхватывает столб.

Рукастый пацан

В этом случае на человека помимо силы трения действует сила реакции
столба. Если человек будет бежать по окружности того же радиуса, то должно выполнятся следующее равенство:







Т.к. в нашем случае человек двигался по окружностям одинакового радиуса с разными скоростями, то отношение скоростей человека в первом и втором случае равно отношению времен, за которые он обогнет столб. Значит








Т.к. k ~ 0,5, а F может спокойно превышать mg, то t2 больше t1 примерно в 1.5 раза.

Значит бегущий человек обхватывает столб рукой, для того чтобы быстрее его обогнуть, т. к. появляется дополнительная сила, действующая со стороны столба на человека, которая увеличивает цетростремительное ускорение человека, в следствие чего увеличивается максимальная возможная скорость, с которой человек может огибать столб.

Задача 2: Как в лесу вытащить застрявшую машину, имея только трос?

Теоретически, по общему алгоритму решения качественных задач, первым делом мы должны написать, в каких условиях рассматривается задача, но у меня мало соображений по этому поводу. Стоит сказать, что трос у нас очень крепкий ( не рвется ни при каких наших последующих действиях ) и мы его можем натянуть так сильно, что сила натяжения в любой точке троса будет одинакова. Также трос почти нерастяжим.

Что же делать с тросом и застрявшей машиной в лесу? Я очень долгое время думал, что один конец троса можно обматать вокруг колеса, другой привязать к дереву, и, после этого включив двигатель, машина будет вытащена. Но сейчас я больше склоняюсь к идее, которую прочитал в Интернетах:
Привяжем один конец троса, а другой — к любой части автомобиля. Выглядит это примерно так:

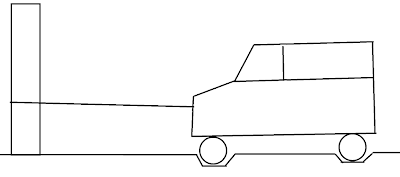Российские дороги...

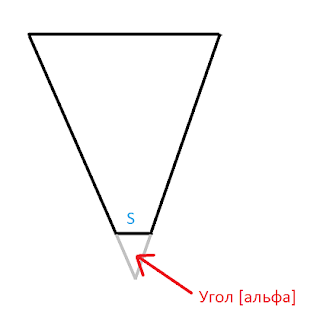
Теперь потянем за середину троса в направлении, перпендикулярном его положению. И, о чудо, машина вытянулась ( по легенде ). Вот картинка процесса, в результате которого происходит данное чудо:

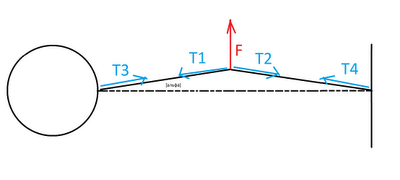Магия прям...

 Когда мы тянем за трос, то он отклоняется от своего начального положения на угол [альфа]. Т.к. сила натяжения троса в каждой точке одинакова, то |T1| = |T2| = |T3| = |T4| = T.
Значит

Т.к. трос почти нерастяжим, то [альфа] << 1 ( в радианах ). Т.е. k*[альфа] = 1, где k > 10.
Т.к. [альфа] – мал, то T = F / 2[альфа] => T > 5F.
Таким образом данная конструкция дает выигрыш более чем в 5 раз.