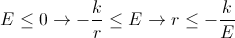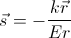Векторизация в ACM

Итак, ACM почти закончился для меня. Лето я провожу бездарно. Поэтому решил что-нибудь написать в блог, чтобы принести хоть какую-то пользу.

Вообще, мне давно были интересно разобраться с SSE/AVX инструкциями. Пару раз я встречал на Codeforces очень сложные кодины (например http://codeforces.com/contest/573/submission/12760770), которые выглядели(да и до сих пор выглядят) для меня как черная магия. Я попытался разобраться с этой магией. Попытаюсь рассказать о том, с чем я разбирался, хоть и похож я больше на шарлатана, чем на мага.

Про быстрое пересечение полуплоскостей и диаграмму Вороного

Наконец-то дошли руки до написания этой статьи. Здесь я хочу в первую очередь поговорить о нахождении пересечения полуплоскостей за O(nlogn).

Код, который я приведу в этой статье, проверен на задаче с Тимуса, но есть вероятность, что в нем содержатся баги для общей задачи пересечения полуплоскостей. Поэтому будьте внимательны ;)

Итак, еще раз суть алгоритма в нескольких пунктах:

• Сначала добавим к нашим полуплоскостям 4 дополнительные - эти полуплоскости будут образовывать так называем bounding-box. Данное действие избавит от лишней возни с бесконечными пересечениями и т.п.
• Дальше нужно отсортировать все полуплоскости по углу их нормального вектора.
• Теперь будем добавлять полуплоскости в таком порядке и после каждого добавления будем поддерживать дэк полуплоскостей, которые образуют стороны многоугольника пересечения.
• Добавляя новую полуплоскость мы, возможно, должны выкинуть часть полуплоскостей с обоих концов дэка. 

Остается еще пару моментов, которые не оговорены в этом списке.

   Во-первых, как можно понять, что пересечение пусто? Предположим, что после добавления новой полуплоскости пересечение стало пусто. Наш алгоритм, в этом случае, выкинет все полуплоскости из дэка кроме одной. Также заметим, что т.к. мы добавили bounding-box, то векторное произведение соседних полуплоскостей в дэке всегда имеет одинаковый знак, который соотносится с порядком сортировки полуплоскостей (по часовой или против). Поэтому если векторное произведение последней полуплоскости в дэке с новой полуплоскостью "плохое", то пересечение пусто. Таким образом, с этим вопросом как-то разобрались.

Рассмотрим такую ситуацию.

Добавилась черная полуплоскость и пересечение стало пусто.

После работы первой части алгоритма были выкинуты полуплоскости Second и Third. Видно, что векторное произведение оставшихся плохое(сортировали против часовой стрелки, векторное произведение меньше 0)

Еще один вопрос - всегда ли нужно добавлять полуплоскость в дэк?
Мне показалось, что достаточно следующего условия: добавлять полуплоскость нужно только в том случае, если первая полуплоскость в дэке содержит (строго содержит) точку пересечения прямых, образующих новую полуплоскость и последнюю полуплоскость в дэке.

Полуплоскость First не содержит в себе точку А - добавлять черную полуплоскость в дэк не надо.

Обратная ситуация - добавить надо.

Вроде бы это все. И в конце этой части статьи привожу код:

//You should normalize plane normal vectors for avoiding problems with precision
Plane pl[N], res[N];
int half(const Point &v)
{
 if (Gr(v.y, 0) || (Eq(v.y, 0) && Gr(v.x, 0)))
  return 1;
 return 2;
}

bool cmpPlane(const Plane &a, const Plane &b)
{
 if (half(a.v) != half(b.v))
  return half(a.v) < half(b.v);
 if (!Eq(a.v * b.v, 0))
  return a.v * b.v > 0;
 return b.contain(a.M);
}

bool eqPlane(const Plane &a, const Plane &b)
{
 return Eq(a.v * b.v, 0);
}

int halfPlaneIntersect(Point *pts)
{
 //Add bounding-box
 Point box[4];
 box[0] = Point(-MAXC, -MAXC);
 box[1] = Point(MAXC, -MAXC);
 box[2] = Point(MAXC, MAXC);
 box[3] = Point(-MAXC, MAXC);
 for (int i = 0; i < 4; i++) pl[cntPl++] = Plane(box[i], box[(i + 1) % 4] - box[i]);
 
 //Sort plane and delete planes with same normal vectors
 sort(pl, pl + cntPl, cmpPlane);
 cntPl = unique(pl, pl + cntPl, eqPlane) - pl;
 
 //Main part of algorithm
 int l = 0, r = 0;
 for (int i = 0; i < cntPl; i++)
 {
  while (r - l > 1 && !pl[i].contain(res[r - 1].getPoint(res[r - 2])))
   r--;
  while (r - l > 1 && !pl[i].contain(res[l].getPoint(res[l + 1])))
   l++;
  if (r - l > 0 && LsEq(res[r - 1].v * pl[i].v, 0))
   return 0;//Empty intersection
  if (r - l < 2 || res[l].contain(pl[i].getPoint(res[r - 1])))
   res[r++] = pl[i];
 }
 //Create result polygon
 int cntPts = 0;
 for (int i = l; i < r - 1; i++)
  pts[cntPts++] = res[i].getPoint(res[i + 1]);
 pts[cntPts++] = res[l].getPoint(res[r - 1]);
 return cntPts;
}

В приведенном коде опущены реализации классов Point и Plane.
Также нельзя оставлять без внимания возможные проблемы с точностью, избежать некоторые из которых можно предварительно отнормировав нормальные вектора плоскостей на единчную длину (спасибо Илье Кучумову за то, что обратил на это внимание).
Плоскость в данной реализации я задаю точкой (M), принадлежащей прямой, образующей плоскость, и направляющим вектором(v) (причем таким, что все точки, принадлежащие плоскости, удовлетворяют условию v * (P - M) >= 0; где * - векторное произведение).
Скажу также, что класс Plane содержит в себе два метода - getPoint(Plane) и contain(Point). Первый возвращает точку пересечения прямых, образующих плоскости; второй - проверяет, принадлежит ли данная точка полуплоскости (строгой полуплоскости).

Также, забыл упомянуть, что данная функция не найдет вырожденных пересечений (точка или отрезок).

Однако, если нужно построить диаграмму Вороного, то таких вырожденных случаев не встретится, и этот код вполне удовлетворяет требованиям задачи.

Ура! Мы научились строить диаграмму Вороного за O(n²logn)!

Немного кода по диаграмме Вороного

В этом посте я хочу разобрать реализацию алгоритма построения диаграммы Вороного за O(n³).
Вспомним на словах саму суть алгоритма:

1. Для каждой точки, как обычно, строим ячейку Вороного. В данном случае мы хотим строить её за O(n²).
2. Будем поддерживать многоугольник, полученный пересечением первых i полуплоскостей (что это за полуплоскости и откуда они взялись можно узнать в предыдущем посте).
3. Добавлять новую полуплоскость будем за O(n), пользуясь тем фактом, что многоугольник пересечения не сильно меняется при добавлении новой полуплоскости.

Сразу скажу, что свой алгоритм я тестировал на задаче Империя наносит ответный удар с Тимуса. Вы тоже можете сдать её после прочтения данного поста.
Собственно, ниже представлен кусок кода, добавляющий очередную полуплоскость и перестраивающий многоугольник пересечения.  

Point hull[N];
Point globP, globV;

bool badPoint(const Point &A)
{
 return Ls((A - globP) % globV, 0); 
}

void addPoint(Point A, int pos, int &n)
{
 for (int i = n; i > pos; i--)
  hull[i] = hull[i - 1];
 hull[pos] = A;
 n++;
}

// A - точка, принадлежащая прямой, образующей полуплоскость
// u - нормальный вектор этой прямой
// r - количество точек в многоугольнике
void addHalfPlane(Point A, Point u, int &r) 
{             
 globP = A;
 globV = u;
 for (int i = 0; i < r; i++)
 {
  Point B = hull[i];
  Point C = hull[(i + 1) % r];
  Point P;
  if (intersectLine(B, C - B, A, u.ort(), P))
  {
   if (onSegment(B, C, P) && B != P && C != P)
    addPoint(P, i + 1, r);
  }
 }
 r = remove_if(hull, hull + r, badPoint) - hull;
}

Поясню некоторые моменты:

1. hull[] - массив, в котором хранится наш многоугольник пересечения
2. addPoint() - insert в массив
3. badPoint() - функция, которая возвращает true, если точка не принадлежит текущей полуплоскости

Наверное стоит отдельно упомянуть о стандартных функциях, использующихся в данном куске кода:

1. intersectLine(A, v, B, u, P) - возвращает true, если прямые пересекаются и сохраняет в P искомую точку. В противном случае, возвращает false.
2. onSegment(A, B, P) - проверяет, правда ли, что точка P лежит на отрезке [A;B]
3. Также, в данном коде используется переопределенный оператор % для двух точек, который обозначает скалярное произведение векторов.

Осталось добавить часть кода, вызывающую функцию addHalfPlane(...) и реализация алгоритма готова:

void solve(Point A, int n)
{
 int r = 0;  
        hull[r++] = Point(0, 0);
 hull[r++] = Point(INF, 0);
 hull[r++] = Point(INF, INF);
 hull[r++] = Point(0, INF);

 for (int i = 0; i < n; i++)
 {
  if (p[i] == A)
   continue;
  Point M = (p[i] + A) / 2.;
  Point u = (A - p[i]);
  addHalfPlane(M, u, r);
 }
}

В начале я также добавил 4 точки - bounding box - которые будут ограничивать мою "бесконечную" плоскость. Это самый удобный и простой способ избавиться от "бесконечных" многоугольников и подобных неприятных вещей.

Собственно, на этом заканчивается данный пост. Надеюсь, в дальнейшем появится продолжение =)

Немного слов про диаграмму Вороного.

Я решил разделить описание алгоритмов с их реализациями. Поэтому здесь описаны только алгоритмы без примеров и замечаний к реализации. 
Определение диаграммы Вороного процитирую с Википедии:

Диаграмма Вороного конечного множества точек S на плоскости представляет такое разбиение плоскости, при котором каждая область этого разбиения образует множество точек, более близких к одному из элементов множества S, чем к любому другому элементу множества.

Опишу несколько свойств диаграммы Вороного, которыми я скорее всего буду пользоваться дальше:

1.  Диаграмма Вороного - это планарный граф. С помощью теоремы Эйлера можно несложно доказать, что если диаграмма Вороного построена на множестве из n точек, то она содержит O(n) ребер и вершин (я знаю доказательство, которое использует тот факт, что степень каждой вершины хотя бы 3).
2. Ячейка диаграммы Вороного для точки P является пересечением полуплоскостей, образованных серединными перпендикулярами отрезков вида [A;P] (A - точка из нашего множества) и содержащих точку P.

Синим выделена ячейка Вороного для точки G
edge - это ребро диаграммы Вороного
vertex - вершина

Все приведенные ниже алгоритмы будут строить лишь множество ячеек Вороного, не объединяя их в общий планарный граф.
Соответственно, самый просто алгоритм за O(n⁴)

1. Зафиксируем точку, ячейку Вороного которой мы хотим построить - точка P.
2. Построим все серединные перпендикуляры отрезков вида [A;P].
3. Пересечем все серединные перпендикуляры между собой.
4. Для каждой точки пересечения проверим, что она принадлежит каждой полуплоскости. Точку, лежащую во всех полуплоскостях, назовем подходящей.
5. Отсортируем все подходящие точки по полярному углу.
6. Полученное множество точек - ячейка Вороного точки P.

    Видно, что для каждой точки ячейка построится за время O(n³) (для каждой из точек пересечения, которых порядка n², мы делаем проверку за n; алгоритм сортировки в таком случае не портит асимптотику).

    Из картинки видно, что ячейка Вороного может быть бесконечной. Данный случай можно определить однозначно по существованию "разрыва" - пары последовательных точек в нашем отсортированном списке, угол между которыми не меньше 180°.

угол обозначенный зеленым цветом - "разрыв"

    Далее разберем на словах алгоритм за O(n³).
В основе этого алгоритма лежит идея пересечения n полуплоскостей за квадрат. Как это делать?
Известно, что пересечение полуплоскостей - это выпуклый многоугольник (возможно бесконечный, как на рисунке). Тогда алгоритм пересечения за квадрат следующий:

1. На i-ой итерации алгоритма будем строить многоугольник, являющийся пересечением первых i полуплоскостей.
2. Чтобы перейти от i-ой итерации к следующий нужно пересечь текущий многоугольник с полуплоскостью. Это можно сделать за время, пропорциональное текущему количеству вершин в многоугольнике. Для этого заметим, что новый многоугольник - это некоторая непрерывная последовательность вершин старого многоугольника и, иногда, ещё две новые вершины по краям (для лучшего понимания можно попробовать исследовать рисунок).

Пересекаем многоугольник с зеленой полуплоскостью

Вуа-ля! Пересекли. Добавились точки J, K. От старого многоугольника остались точки E, D, C.

    Дальше - больше! Перед Вашими глазами сейчас предстанет алгоритм алгоритм за O(n²logn).
    Идея та же, что и в предыдущем алгоритме - пересечение полуплоскостей. Только можно сделать это оптимальнее - за nlogn. 
    Вспомним, что у нас есть. Мы для каждой точки хотим пересечь n полуплоскостей за nlogn. Заметим, что многоугольник пересечения полуплоскостей можно задавать массивом полуплоскостей, обладающим таким свойством - точка пересечения прямых, образующих пары соседних полуплоскостей - это вершина искомого многоугольника (см. рисунок для лучшего понимания).

Выделенный многоугольник можно задать последовательностью

 I, III, IV, V

    Идея алгоритма состоит в следующем:

1. Отсортируем полуплоскости по углу нормального вектора. (в случае равенства угла порядок полуплоскостей не будет иметь значения).
2. Будем поддерживать массив полуплоскостей, задающий многоугольник-пересечения первых i полуплоскостей (уже отсортированных).
3. Чтобы добавить новую полуплоскость нам, возможно, понадобится удалить несколько последних вершин текущего многоугольника, т.к. они не принадлежат новой полуплоскости.
4. В конце нужно добавить новую полуплоскость в конец массива.

Заметим, что наш массив - это стэк (т.к. мы только удаляем с конца и добавляем в конце).

Ниже приведена gif-анимация процесса построения пересечения полуплоскостей (они пронумерованы римскими числами в порядке сортировки).

В процессе добавления полуплоскости III мы должны удалить полуплоскость II, т.к. она добавляет плохую точку BADPOINT

    Асимптотика данного алгоритма складывается из двух частей:

1. Отсортировать все полуплоскости - O(nlogn)
2. Пробег по отсортированному массиву с добавлением и извлечением из стэка. Заметим, что каждая полуплоскость будет добавлена в стэк ровно 1 раз, соответственно удалена тоже не больше одного раза. Итого данная часть алгоритм работает за O(n).

    И наконец, последний алгоритм, который я хотел затронуть (и который я в силах осознать) - это алгоритм за O(n²).
 В данном алгоритме используется тот факт, что количество ребер в диаграмме Вороного - O(n).
Действительно, если бы мы научились находить каждое ребро одной ячейки Вороного за время T(n), то мы автоматически придумываем алгоритм построения диаграммы Вороного за O(n T(n)). Круто =)
    Давайте начнем придумывать. Для начала хочется от чего-то оттолкнуться. Действительно, найдем такую точку, которая по любому есть в ячейке Вороного для данной точки. Эта точка несложно ищется - давайте среди всех середин отрезков M = (середина [P;A], где P - выбранная точка, A - любая другая точка из исходного множества) выберем ближайшую. Утверждается, что эта точка точно присутствуем в ячейке для точки P (т.е. она лежит на границе многоугольника, который мы хотим найти). Если таких точек несколько - возьмем любую.

K - ближайшая точка для G

    Замечательно, теперь у нас есть опорная точка и опорная прямая, т.к. серединный перпендикуляр отрезка, на котором мы взяли ближайшую точку, является ребром результирующего многоугольника.

    Теперь поймем, как по прямой, содержащей ребро ответа и точке на ребре узнать следующее ребро. Ну это не сильно сложно. Давайте пересечем все остальные серединные перпендикуляры с текущей прямой. Возьмем 2 (или 1) точки пересечения - самый ближайшие точки с каждой из сторон к текущей точке на ребре (см. рисунок срочно!):

Разберем немного рисунок. Точка K - опорная точка. Мы пересекли четыре серединных перпендикуляра. P, Q - точки пересечения с прямой f, причем самые ближайшие к точке K. Понятно - что эти точки являются вершинами конечного многоугольника, а серединные перпендикуляры, их содержащие - следующими ребрами. Поэтому достаточно запустить рекурсивную функцию от изменившихся параметров - точки P и прямой n и точки Q и прямой j. 

    Не нужно забывать про то, что несколько серединных перпендикуляров могут пересекать прямую в одной точке. В таком  случае нужно выбрать тот серединный перпендикуляр, который "круче" заворачивает вокруг исходной точки(около которой строим ячейку).

    Более формально, угол между направлением нового ребра и направлением на точку, около которой строим ячейку, должен быть минимален (на рисунке выделен зеленым).

    Таким образом, мы каждое ребро мы научились строить за O(n). Т.е. итоговая асимптотика такая, какую я заявил в начале рассказа про этот алгоритм =)

    На этом данный пост кончается. Мне кажется в нем даже чересчур много инфы.
Хочу напомнить, что в данном посте я не стремился указать на способы реализации описанных алгоритмов. Моей задачей было ознакомить читателя с идеями =)

Доказательство первого закона Кеплера

(на данный момент в этой статье есть много недочетов. я постараюсь исправить это в ближайшее время)

  Наверное, в поисках адекватного доказательства этого закона, я перерыл многие сайты рунета. Однако больше того, что нам рассказали в СУНЦ-е я не нашел, а доказательство рассказанное нашим учителем меня не совсем устраивает.
   И вот сегодня я решил поискать информацию об этом законе в англоязычных источниках. Во-первых, на запрос "proof of Kepler's first law" Google сразу выдал кучу полезных сайтов, в то время как на аналогичный русский запрос поисковые системы находят лишь формулировку этого закона или что-то наподобие "Закон Кеплера - доказательство существования эфира"...

Открыв наиболее понятную статью, я решил разобраться с доказательством. Мне кажется, что это у меня удалось и в этом посте я хочу изложить то доказательство, которое я прочитал (вот ссылка на оригинал).

Итак, сначала оговорим некоторые математические факты, которыми мы будем пользоваться, но доказывать не будем, т.к это чистая математика:

Теперь приступим к самому доказательству.

Рассмотрим полную энергию планеты, обращающейся вокруг некоторой звезды, и находящаяся в данный момент на расстоянии r.

1

Т.к. на систему не действует внешних сил, то энергия сохраняется.

Покажем, что при E <= 0, расстояние от звезды до планеты ограничено.

В самом деле:

2

Таким образом, движение планеты ограничено сферой, с центром в точке O(звезда) и радиусом 

R = -k / E.

Теперь рассмотрим планету, двигающуюся по траектории Q.

Также построим окружность C радиусом R = -k / E.

Заметим, что планета такой же массы, как наша, находящаяся в точке s(и не обладающая кинетической энергией) имеет такую же энергию, как планета, движущаяся по траектории Q и находящаяся в точке r (точки O, s, r лежат на одной прямой). Данное равенство следует из выбора радиуса окружность C.

Обозначим через s - радиус вектор проведенный из точки O в точку s. Тогда s:

3

Построим на рисунке прямую L, совпадающую по направлению с вектором импульса тела(т.е. с вектором скорости) и проходящей через точку r. 

Построим также точку, симметричную точке s относительно прямой L - точку t.

Также на прямой N отметим точку n, такую, что n = L x p

Теорема: вектор t(Ot) постоянен и равен K/mE, где 

4

Доказательство:

Заметим, что вектор t можно получить путем вычитания из вектора s двух векторов j, являющимися проекциями вектора (s - r) на прямую N, которая перпендикулярна прямой L(данный вывод следует из построения точки t, как симметричной точке s относительно прямой L).

Значит:

5

Т.к. (s - r) * n / n  - это проекция вектора (s - r) на прямую N. А n / n - нормированный вектора, направленный вдоль прямой N.

Найдем, чему равно (s - r) * n (подставив значение вектора n и s):

n * n = (L x p) ^ 2 = L^2 * p^2 (это следует из того, что вектор L ортогонален вектору p).

Значит вектор t равен:

Заметим, что вектор t неизменен, т.к. (это я не понял, но к сожалению осознание этого пришло только в момент написания этой строчки. Завтра постараюсь понять и допилить).

Ну и как бы теорема доказана.

Из данной теоремы следует, что

|r - t| + |r - O| = |r - s| + |r - O| = |s|. Т.к. |s| - константа, то мы доказали, что в любой момент сумма расстояний от планеты до двух фиксированных точек - константа. Значит это эллипс. ч.т.д.

Как слить контест или "Первая личная олимпиада 2012/2013"

   Совсем недавно закончилась первая личная олимпиада этого учебного года (Результаты, задачи).

   В последнее время я чувствую себя не таким уж и дном, поэтому настрой на этот контест был вполне боевой. 

   Началась олимпиада для меня довольно странно. Прочитав задачу A, я быстро написал какую то лажу (ну как быстро, за минут 20 сдал, т.к. у меня начал жутко тормозить настольный компьютер и пришлось быстро включать ноут).

   Задача B мне понравилась. Я довольно быстро додумался до главной идеи, но окончательная реализация (на 36 баллов) была дописана мною за 2 часа до конца контеста.

   Прочитав задачу C я немного удивился, т.к. там был капитан(даже легче чем A). Однако, я до сих пор не разобрался почему, у меня не проходит 1 тест, из-за чего за эту задачу я получил 98 баллов, что меня не сильно расстроило.

   Задача D самая клевая задача контеста. Я не придумал полного решения, но за 1.5 часов до конца, у меня была какая то идея, проходящая группу тестов на 60 баллов. Я уложился в это время, реализовав почти то, что придумал(оказалось, что я не совсем правильно понял условие). Однако, посмотрев на результаты, я увидел что у меня за эту задачу 5 баллов.

  Погрузившись в грусть, тоску и архив с тестами жюри я начал искать баги в задачах B и D. Каково было мое удивление, когда я вспомнил, что хотел "не забыть запилить long long в задачу D". Впиливаю long long - проходить 12 тестов, т.е ровно те 60 баллов, которые я планировал.

С задачей B я разбирался дольше. Однако обнаружив свою ошибку начал сильно негодовать из-за своей криворукости. Баг заключался в том, что у меня существовала функция myFind(...), которая возвращала -1, если не находила нужный элемент в массиве. Однако при проверке, нашелся ли данный элемент в массиве, я написал следующую строчку:

if (myFind(..) == 1) {//do something}

После чего без сомнений признал этот баг самым нелепым за всю мою историю сливов контестов.

Итог - 30 место с очень низким количеством баллов. За задачу B обидно...

//P.S. Через час после того, как я написал пост, на Codeforces появился этот контест в разделе "Тренировки". Отправив свое решение по B с исправленной -1, я получил вердикт "Полное решение"

Качественные задачи. Часть 5

 Почему крученая шайба преодолевает большее расстояние, чем не крученая?

Будем считать, что на шайбу не дейстувет сила сопротивления воздуха, т.к. она во много раз меньше силы трения скольжения шайбы об лед.

Тогда рассмотрим, как действуют силы на маленький кусочек шайбы:

Сила трения направлена против относительного перемещения. В нашем случае лед не движется, значит сила трения направлена против скорости.

Видно, что сила трения, помимо того, что уменьшает энергию центра масс, также уменьшает энергию данного кусочка относительно центра масс. Такое утверждение истинно для каждого элемента шайбы. Тогда запишем теорему о изменении кинетической энергии, воспользовавшись теоремой Кёнига:

c.o.f - центр масс. fric. - трение. E' - энергий в системе отсчета, относительно центра масс

Т.к. при движении шайбы без вращения изменение кинетической энергии относительно центра масс всегда равно 0 ( т.к. относительно центра масс - шайба неподвижна ), значит при одном и том же перемещении изменение кинетической энергии центра масс в случае вращения будет меньше, чем в случае поступательного движения шайбы. Таким образом, в случае вращения шайбы, сила трения должна совершить большую работу, чтобы остановить шайбу, а значит совершить большее перемещение.

Значит закрученная шайба пролетит большее расстояние, т.к. часть работы силы трения будет уходить на измнение кинетической энергии шайбы относительно центра масс, в то время, как без закручивания, эта работа пошла бы на остановку центра масс.

P.S. Какое-то ужасное и громоздкое решение довольно несложной задачи получилось, господа...